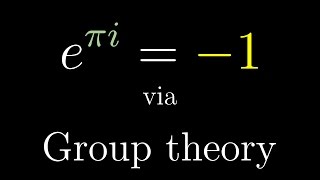–°–Ї–∞—З–∞—В—М —Б —О—В—Г–± –Э–∞—Б—В–Њ—П—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞ —Н—В–Њ –Э–Х e^iѕА = -1 –≤ —Е–Њ—А–Њ—И–µ–Љ –Ї–∞—З–µ—Б—В–≤–µ
–°–Ї–∞—З–∞—В—М –±–µ—Б–њ–ї–∞—В–љ–Њ –Є —Б–Љ–Њ—В—А–µ—В—М —О—В—Г–±-–≤–Є–і–µ–Њ –±–µ–Ј –±–ї–Њ–Ї–Є—А–Њ–≤–Њ–Ї –Э–∞—Б—В–Њ—П—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞ —Н—В–Њ –Э–Х e^iѕА = -1 –≤ –Ї–∞—З–µ—Б—В–≤–µ 4–Ї (2–Ї / 1080p)
–£ –љ–∞—Б –≤—Л –Љ–Њ–ґ–µ—В–µ –њ–Њ—Б–Љ–Њ—В—А–µ—В—М –±–µ—Б–њ–ї–∞—В–љ–Њ –Э–∞—Б—В–Њ—П—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞ —Н—В–Њ –Э–Х e^iѕА = -1 –Є–ї–Є —Б–Ї–∞—З–∞—В—М –≤ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–Љ –і–Њ—Б—В—Г–њ–љ–Њ–Љ –Ї–∞—З–µ—Б—В–≤–µ, –Ї–Њ—В–Њ—А–Њ–µ –±—Л–ї–Њ –Ј–∞–≥—А—Г–ґ–µ–љ–Њ –љ–∞ —О—В—Г–±. –Ф–ї—П —Б–Ї–∞—З–Є–≤–∞–љ–Є—П –≤—Л–±–µ—А–Є—В–µ –≤–∞—А–Є–∞–љ—В –Є–Ј —Д–Њ—А–Љ—Л –љ–Є–ґ–µ:
–Ч–∞–≥—А—Г–Ј–Є—В—М –Љ—Г–Ј—Л–Ї—Г / —А–Є–љ–≥—В–Њ–љ –Э–∞—Б—В–Њ—П—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞ —Н—В–Њ –Э–Х e^iѕА = -1 –≤ —Д–Њ—А–Љ–∞—В–µ MP3:
–Х—Б–ї–Є –Ї–љ–Њ–њ–Ї–Є —Б–Ї–∞—З–Є–≤–∞–љ–Є—П –љ–µ
–Ј–∞–≥—А—Г–Ј–Є–ї–Є—Б—М
–Э–Р–Ц–Ь–Ш–Ґ–Х –Ч–Ф–Х–°–ђ –Є–ї–Є –Њ–±–љ–Њ–≤–Є—В–µ —Б—В—А–∞–љ–Є—Ж—Г
–Х—Б–ї–Є –≤–Њ–Ј–љ–Є–Ї–∞—О—В –њ—А–Њ–±–ї–µ–Љ—Л —Б–Њ —Б–Ї–∞—З–Є–≤–∞–љ–Є–µ–Љ, –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞ –љ–∞–њ–Є—И–Є—В–µ –≤ –њ–Њ–і–і–µ—А–ґ–Ї—Г –њ–Њ –∞–і—А–µ—Б—Г –≤–љ–Є–Ј—Г
—Б—В—А–∞–љ–Є—Ж—Л.
–°–њ–∞—Б–Є–±–Њ –Ј–∞ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ —Б–µ—А–≤–Є—Б–∞ savevideohd.ru
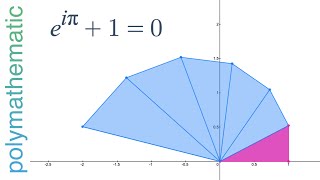
–Э–∞—Б—В–Њ—П—Й–µ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞ —Н—В–Њ –Э–Х e^iѕА = -1
–£ –Љ–µ–љ—П –µ—Б—В—М —Е–Њ—А–Њ—И–∞—П –љ–Њ–≤–Њ—Б—В—М –Є –њ–ї–Њ—Е–∞—П –љ–Њ–≤–Њ—Б—В—М –і–ї—П –≤–∞—Б. –Я–ї–Њ—Е–∞—П –љ–Њ–≤–Њ—Б—В—М –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ –Ј–љ–∞–Љ–µ–љ–Є—В–Њ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –≠–є–ї–µ—А–∞, e^iѕА = -1, –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ –љ–µ —П–≤–ї—П–µ—В—Б—П –µ–≥–Њ —В–Њ–ґ–і–µ—Б—В–≤–Њ–Љ. –•–Њ—А–Њ—И–∞—П –љ–Њ–≤–Њ—Б—В—М вАУ –≠–є–ї–µ—А –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –Њ—В–Ї—А—Л–ї –Њ–≥—А–Њ–Љ–љ—Л–µ —В—Г—З–Є —Д–∞–љ—В–∞—Б—В–Є—З–µ—Б–Ї–Є—Е —В–Њ–ґ–і–µ—Б—В–≤. –≠—В–Њ –≤–Є–і–µ–Њ –±—Г–і–µ—В –љ–∞ —В–µ–Љ—Г —В–Њ–≥–Њ —В–Њ–ґ–і–µ—Б—В–≤–∞, –Ї–Њ—В–Њ—А–Њ–µ —Б–і–µ–ї–∞–ї–Њ –µ–≥–Њ –Ј–љ–∞–Љ–µ–љ–Є—В—Л–Љ, –≤ –Њ–±—Й–µ–Љ-—В–Њ, –Ј–∞ –Њ–і–Є–љ –і–µ–љ—М: ѕА^2/6 = –±–µ—Б–Ї–Њ–љ–µ—З–љ–∞—П —Б—Г–Љ–Љ–∞ –Њ–±—А–∞—В–љ—Л—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ –љ–∞—В—Г—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї. –≠—В–Њ –≤–Є–і–µ–Њ –њ—А–µ–і–Њ—Б—В–∞–≤–Є—В –љ–µ—Е–Є—В—А—Л–є –∞—А–≥—Г–Љ–µ–љ—В –≠–є–ї–µ—А–∞, –Ї–Њ—В–Њ—А—Л–є, –њ–Њ–Љ–Є–Љ–Њ —Н—В–Њ–≥–Њ —Б—Г–њ–µ—А–Є–Ј–≤–µ—Б—В–љ–Њ–≥–Њ —В–Њ–ґ–і–µ—Б—В–≤–∞, –њ–Њ–Ј–≤–Њ–ї–Є–ї –µ–Љ—Г –њ–Њ–і—Б—З–Є—В–∞—В—М —В–Њ—З–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є–Є –і–ї—П –≤—Б–µ—Е —З—С—В–љ—Л—Е —З–Є—Б–µ–ї (–Є –Љ–љ–Њ–≥–Њ–µ –і—А—Г–≥–Њ–µ :) –ѓ –Њ–≥—А–Њ–Љ–љ—Л–є —Д–∞–љ–∞—В –≠–є–ї–µ—А–∞ –Є –і–∞–≤–љ—Л–Љ –і–∞–≤–љ–Њ —Г–ґ–µ —Б–Њ–±–Є—А–∞–ї—Б—П —Б–і–µ–ї–∞—В—М —Н—В–Њ –≤–Є–і–µ–Њ. –Т –Є—В–Њ–≥–µ –≤—Б—С —Б–ї–Њ–ґ–Є–ї–Њ—Б—М –і–Њ–≤–Њ–ї—М–љ–Њ —Е–Њ—А–Њ—И–Њ, —П –і—Г–Љ–∞—О. –Ю–і–љ–∞ –Є–Ј –≤–µ—Й–µ–є, –Ї–Њ—В–Њ—А—Л–µ –Љ–љ–µ –Њ—Б–Њ–±–µ–љ–љ–Њ –љ—А–∞–≤—П—В—Б—П –≤ –Ј–∞–њ–Є—Б—Л–≤–∞–љ–Є–Є —Н—В–Є—Е –≤–Є–і–µ–Њ, вАУ —Н—В–Њ –љ–∞—Б–Ї–Њ–ї—М–Ї–Њ –Љ–љ–Њ–≥–Њ —П –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Г–Ј–љ–∞—О —Б–∞–Љ. –Ъ–Њ–љ–Ї—А–µ—В–љ–Њ –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —П—А–Ї–Є–Љ–Є –Љ–Њ–Љ–µ–љ—В–∞–Љ–Є —Б—В–∞–ї–Є –њ–Њ–і—Б—З—С—В —В–µ—Е –Њ—Б—В–∞–ї—М–љ—Л—Е —Б—Г–Љ–Љ —Б –њ–Њ–Љ–Њ—Й—М—О –Є–і–µ–Є –≠–є–ї–µ—А–∞, –Њ –Ї–Њ—В–Њ—А—Л—Е —П –≥–Њ–≤–Њ—А—О –≤ –≤–Є–і–µ–Њ (–Ј–љ–∞—З–µ–љ–Є—П –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є–Є –≤ —В–Њ—З–Ї–∞—Е —З—С—В–љ—Л—Е —З–Є—Б–µ–ї), –∞ —В–∞–Ї–ґ–µ –Є–Ј—Г—З–µ–љ–Є–µ –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–≥–Њ —Б–њ–Њ—Б–Њ–±–∞ –≤—Л–≤–µ—Б—В–Є —Д–Њ—А–Љ—Г–ї—Г –Ы–µ–є–±–љ–Є—Ж–∞, –Є—Б–њ–Њ–ї—М–Ј—Г—П –љ—Г–ї–Є —Д—Г–љ–Ї—Ж–Є–Є 1-sin(x). –Ю, –Є –µ—Й—С –Ї–Њ–µ-—З—В–Њ. –Ш–і–µ—П –≠–є–ї–µ—А–∞ –Њ –Ј–∞–њ–Є—Б–Є sin(x) –≤ —В–µ—А–Љ–Є–љ–∞—Е –µ–≥–Њ –љ—Г–ї–µ–є –Љ–Њ–ґ–µ—В –њ–Њ–Ї–∞–Ј–∞—В—М—Б—П —Б–ї–µ–≥–Ї–∞ –±–µ–Ј—Г–Љ–љ–Њ–є, –љ–Њ –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В —В–µ–Њ—А–µ–Љ–∞, –Ї–Њ—В–Њ—А–∞—П –≥–Њ–≤–Њ—А–Є—В –≤ —В–Њ—З–љ–Њ—Б—В–Є —В–Њ, —З—В–Њ —В–∞–Ї–Њ–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤ –і–∞–љ–љ–Њ–Љ —Б–Љ—Л—Б–ї–µ. –Ю–љ–∞ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —В–µ–Њ—А–µ–Љ–Њ–є –Т–µ–є–µ—А—И—В—А–∞—Б—Б–∞ –Њ —Ж–µ–ї—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е (Weierstrass factorization theorem). –§—Г—В–±–Њ–ї–Ї–∞, –Ї–Њ—В–Њ—А—Г—О —П –љ–Њ—И—Г –≤ —Н—В–Њ–Љ –≤–Є–і–µ–Њ, —Г –Љ–µ–љ—П –њ–Њ—П–≤–Є–ї–∞—Б—М –Њ—В—Б—О–і–∞: https://shirt.woot.com/offers/pi-rate... –°–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ –Ь–∞—А—В–Є –†–Њ—Б—Б—Г (Marty Ross) –Є –Ф–∞–љ–Є–ї—Г –Ф–Љ–Є—В—А–Є–µ–≤—Г –Ј–∞ –Є—Е –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є –њ–Њ –њ–Њ–≤–Њ–і—Г —А–∞–љ–љ–µ–≥–Њ —З–µ—А–љ–Њ–≤–Є–Ї–∞ —Н—В–Њ–≥–Њ –≤–Є–і–µ–Њ. –Э–∞—Б–ї–∞–ґ–і–∞–є—В–µ—Б—М! –С—Г—А–Ї–∞—А–і (Burkard)