Скачать с ютуб The Hopf Fibration Explained в хорошем качестве

The Hopf Fibration Explained

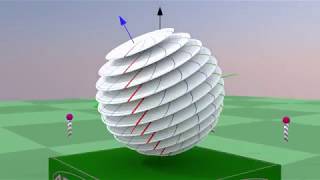
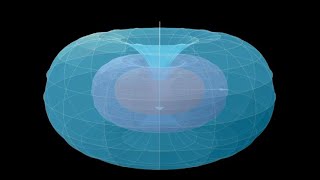
Read a written version of this video in any order that you like: https://iamazadi.github.io/Porta.jl/d... The Hopf fibration is a fiber bundle with a two-dimensional sphere as the base space and circles as the fiber space. It is the geometrical shape that relates Einstein's spacetime to quantum fields. In this model, we visualize the Hopf fibration by first computing its points via a bundle atlas and then rendering the points in 3D space via stereographic projection. The projection step is necessary because the Hopf fibration is embedded in a four-space. Yet, it has only three degrees of freedom as a three-dimensional shape. The idea that makes this model more special and interesting than a typical visualization is the idea of [Planet Hopf]( http://drorbn.net/AcademicPensieve/Pr... ), due to Dror Bar-Natan (2010). The basic idea is that since the Hopf map takes the three-dimensional sphere into the two-dimensional sphere, we can pull the skin of the globe back to the three-sphere and visualize it. Into the bargain, the Earth rotates about its axis every 24 hours. That spinning transformation of the Earth, together with the non-trivial product space of the Hopf bundle, can be encoded naturally into a monolithic visualization. It also makes sense to visualize differential operators in the Minkowski space-time as vectors in a cross-section of the Hopf bundle and then study the properties of spin-transformations. The choice of a gauge transformation (or trivialization) along with Lorentz transformations of Minkowski spacetime should not have any effect on physical laws. It is therefore a great model to understand these transformations and walk the road to reality. The following explains how the source code for generating animations of the Hopf fibration works (alternative views of Planet Hopf). We follow the beginning of chapter 4 of [Mark J.D. Hamilton (2018)]( https://doi.org/10.1007/978-3-319-684... ) for a formal definition of the Hopf fibration as a fiber bundle. The book Mathematical Gauge Theory explains the Standard Model to students of both mathematics and physics, covers both the specific gauge theory of the Standard Model and generalizations, and is highly accessible and self-contained. Then, the definitions are going to be used to explain the source code in terms of computational methods and types. References Physics and Geometry, [Edward Witten]( https://cds.cern.ch/record/181783/fil... ), (1987) The iconic [Wall]( https://scgp.stonybrook.edu/archives/... ) of Stony Brook University [The Road to Reality]( https://www.amazon.com/Road-Reality-C... ), Sir Roger Penrose, (2004) A [Portal](    • A Portal Special Presentation- Geomet...   ) Special Presentation- Geometric Unity: A First Look [Planet Hopf]( http://drorbn.net/AcademicPensieve/Pr... ), Dror Bar-Natan, (2010) [SPINORS AND SPACE-TIME]( https://doi.org/10.1017/CBO9780511564048 ), Volume 1: Two-spinor calculus and relativistic fields, Roger Penrose, Wolfgang Rindler, (1984) [A Young Person's Guide to the Hopf Fibration]( https://arxiv.org/abs/0908.1205 ), Zachary Treisman, (2009) [Mathematical Gauge Theory]( https://doi.org/10.1007/978-3-319-684... ), with Applications to the Standard Model of Particle Physics, Mark J.D. Hamilton, (2018) [Dynamics in the Hopf bundle]( https://personalpages.surrey.ac.uk/t.... ), the geometric phase and implications for dynamical systems, Rupert Way, (2008)