Скачать с ютуб Particle in a 1D Box | Infinite Potential Well Problem in QM в хорошем качестве

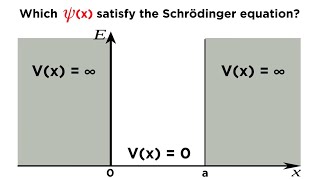
Particle in a 1D Box | Infinite Potential Well Problem in QM

The Infinite Potential Well problem is one of the most important and simplest problems in Quantum Mechanics. In this video, I do a complete discussion on the topic. 𓏬𓏬𓏬𓏬𓏬ELEVATE CLASSES𓏬𓏬𓏬𓏬𓏬 Browse LIVE & Recorded Courses for Physics IITJAM, CSIR-NET, GATE, TIFR, JEST etc on our platform ► https://www.elevateclasses.in/ Android ► https://bit.ly/3zU71ur iOS ► https://apple.co/3ZPRWVJ (use ORG code - AHGXS) 𓏬𓏬𓏬𓏬𓏬LEC NOTES - GDRIVE𓏬𓏬𓏬𓏬𓏬 Find the PDF Scanned copy of my NOTES for this lecture here: 𓏬𓏬𓏬𓏬𓏬VIDEO DESCRIPTION𓏬𓏬𓏬𓏬𓏬𓏬 The particle in a box problem considers a single particle, such as an electron, trapped in a one-dimensional region between two impenetrable walls. The walls are so high that the particle cannot escape, meaning its potential energy is zero inside the box and infinitely large outside. Wavefunction: In quantum mechanics, the state of the particle is described by a wavefunction. This wavefunction represents the probability amplitude of finding the particle at a specific position within the box. Inside the box, the wavefunction must meet certain boundary conditions: it must be zero at the walls of the box because the particle cannot exist outside the box. Quantization: Unlike in classical mechanics, where the particle can have any energy, the particle in a box can only have specific, discrete energy levels. These energy levels are quantized and are determined by the size of the box and the mass of the particle. Nodes and Antinodes: The wavefunction inside the box exhibits a pattern of nodes (points where the wavefunction is zero) and antinodes (points where the wavefunction has maximum amplitude). The number of nodes increases with the energy level, indicating higher energy states correspond to more complex wave patterns. Energy Levels: The lowest energy state, called the ground state, has the simplest wavefunction with no nodes (except at the boundaries). Higher energy states, called excited states, have increasing numbers of nodes. The spacing between energy levels increases as the particle's energy increases. This problem illustrates fundamental quantum mechanical principles, such as quantization of energy and the wave nature of particles. It also serves as a basis for understanding more complex systems in quantum mechanics, including atoms and molecules. 00:00 Introduction 01:53 Solution of Time Independent Schrodinger's Eqn 06:43 Boundary Conditions 10:48 Discrete Energy Levels 17:32 Normalization & Wavefunction 24:23 Visualization of Eigenfunction & Probabilities 30:07 Properties of Eigenfunction Sulutions 𓏬𓏬𓏬𓏬𓏬𓏬TELEGRAM𓏬𓏬𓏬𓏬𓏬𓏬 Join my Telegram Channel ► https://t.me/FortheLoveofPhysicsYT 𓏬𓏬𓏬𓏬𓏬SUPPORT CHANNEL𓏬𓏬𓏬𓏬𓏬 Your Financial support provides me an additional incentive to create high quality lecture videos. I am very much thankful for your generosity and kindness Support/ Patreon ❤️❤️❤️  / dibyajyotidas   Donate/ Paypal 🔥🔥🔥 https://paypal.me/FortheLoveofPhysics JOIN MEMBERSHIP in Youtube 😇😇😇    / @fortheloveofphysics