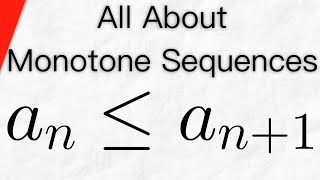Скачать с ютуб Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis в хорошем качестве

Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis

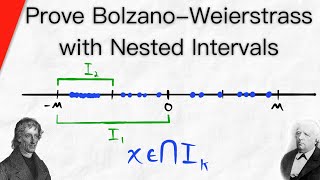
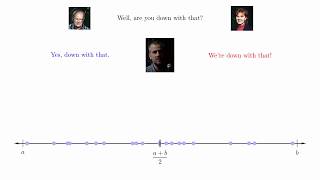
Every bounded sequence has a convergent subsequence. This is the Bolzano-Weierstrass theorem for sequences, and we prove it in today's real analysis video lesson. We'll use two previous results that make this proof short and easy. First is the monotone subsequence theorem, stating that every sequence has a monotone subsequence. Then we finish things off with the monotone convergence theorem, telling us a monotone sequence converges if and only if it is bounded. #RealAnalysis Proof Every Sequence has a Monotone Subsequence (Monotone Subsequence Theorem):    • Monotone Subsequence Theorem (Every S...   Proof of Monotone Convergence Theorem:    • Detailed Proof of the Monotone Conver...   Bolzano-Weierstrass Theorem for Sequences: (coming soon) Proving Bolzano-Weierstrass with Nested Intervals:    • Proving Bolzano-Weierstrass with Nest...   Real Analysis Playlist:    • Real Analysis   ★DONATE★ ◆ Support Wrath of Math on Patreon for early access to new videos and other exclusive benefits:   / wrathofmathlessons   ◆ Donate on PayPal: https://www.paypal.me/wrathofmath Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon! Thanks to Crayon Angel, my favorite musician in the world, who upon my request gave me permission to use his music in my math lessons: https://crayonangel.bandcamp.com/ Follow Wrath of Math on... ● Instagram:   / wrathofmathedu   ● Facebook:   / wrathofmath   ● Twitter:   / wrathofmathedu   My Music Channel:    / @emery3050