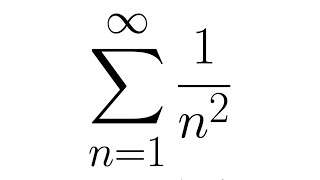Скачать с ютуб Analytic Continuation and the Zeta Function в хорошем качестве

Analytic Continuation and the Zeta Function

Where do complex functions come from? In this video we explore the idea of analytic continuation, a powerful technique which allows us to extend functions such as sin(x) from the real numbers into the complex plane. Using analytic continuation we can finally define the zeta function for complex inputs and make sense of what it is the Riemann Hypothesis is claiming. If you would like to support the production of our content, we have a Patreon! Sign up at   / zetamath   Visit our second channel!    / zetamathdoespuzzles   Links: Blog post by Terry Tao: https://terrytao.wordpress.com/2010/0... Mathologer: Ramanujan: Making sense of 1+2+3...=-1/12 and Co:    • Ramanujan: Making sense of 1+2+3+... ...   Chapters: 00:00 zetamath does puzzles 00:23 Recap 02:40 Bombelli and the cubic formula 08:45 Evaluating real functions at complex numbers 12:33 Maclaurin series 21:22 Taylor series 27:19 Analytic continuation 35:57 What goes wrong 48:19 Next time Animations in this video were created using Manim Community. For more information, visit https://manim.community Thanks to Keith Welker for our theme music.