Скачать с ютуб Derivatives... What? (NancyPi) в хорошем качестве

Derivatives... What? (NancyPi)

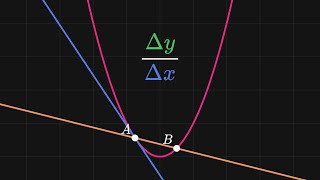
MIT grad shows the DEFINITION of the derivative and how to FIND the derivative using that limit definition. To skip ahead: 1) For what the derivative MEANS, skip to 0:23. 2) For the SLOPE OF THE SECANT line, skip to 2:53. 3) For the SECANT BECOMING THE TANGENT and DEFINITION OF THE DERIVATIVE, skip to 5:54. 4) For how to FIND THE DERIVATIVE USING THE (LIMIT) DEFINITION of the derivative, skip to 10:28. Nancy formerly of MathBFF explains the steps. For my video on the shorter, faster DERIVATIVE RULES for how to take a derivative, jump to:    • Derivatives... How? (NancyPi)   Follow Nancy on Instagram:   / nancypi   Twitter:   / nancypi   INTRODUCTION to derivatives: 1) WHAT IS THE DERIVATIVE? It's a function that tells you the slope (of the line tangent to the curve) at every point. Another way to think of it is that the derivative gives you the rate of change at any instant (the "instantaneous rate of change" at each point). You can find the derivative either with the proper DEFINITION OF THE DERIVATIVE ("by the limit process") or the faster, simpler way with the shortcut derivative rules such as the Power Rule, Product Rule, Quotient Rule, and Chain Rule. This video shows the first way, with the DEFINITION of the derivative, and how to use it to calculate the derivative. 2) SLOPE OF SECANT: To make the definition of the derivative, we can start with the slope of the straight secant line through a point x and some other point nearby, h distance away horizontally. If we label the two points and use the slope formula to write an expression for the slope of this secant line, the expression you get is [f(x+h) - f(x)] / h, which is also known as the DIFFERENCE QUOTIENT. 3) DEFINITION OF DERIVATIVE: That straight line slope we just found is actually a decent ESTIMATE for the slope at x, but it's not really the slope at x. We can get the EXACT slope of the tangent line at x by closing in on x and narrowing h to zero, by taking the LIMIT of the secant slope, as h approaches 0. The slope of the secant line becomes the slope of the tangent line. Not only is this limit equal to the slope of the tangent line, it is the definition of the derivative (when the limit exists) or f'(x). 4) HOW TO FIND THE DERIVATIVE OF A FUNCTION USING (LIMIT) DEFINITION: If you have to find the derivative "using the definition of the derivative" or "by the limit process", then you can use the limit definition we just found for any f(x) equation you're given. Remember that the f(x+h) part of the formula means to replace x with (x+h) anywhere x appears in the function f(x). If you want help knowing how to find the limit at the end, you can jump to my video "How to Find Any Limit":    • How to Find Any Limit (NancyPi)   For an intro to the concept of limits, jump to:    • Introduction to Limits (NancyPi)   For more of my math videos for calculus, precalculus, and algebra, check out: http://nancypi.com