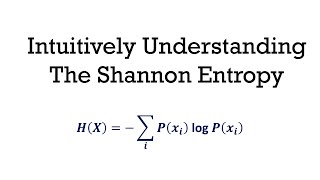Скачать с ютуб Understanding Shannon entropy: (1) variability within a distribution в хорошем качестве

Understanding Shannon entropy: (1) variability within a distribution

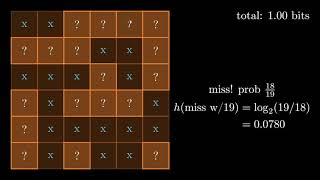
In this series of videos we'll try to bring some clarity to the concept of entropy. We'll specifically take the Shannon entropy and: show that it represents the variability of the elements within a distribution, how different are they from each other (general characterization that works in all disciplines) show that this variability is measured in terms of the minimum number of questions needed to identify an element in the distribution (link to information theory) show that this is related to the logarithm of the number of permutations over large sequences (link to combinatorics) show that it is not in general coordinate independent (and that the KL divergence does not fix this) show that it is coordinate independent on physical state spaces - classical phase space and quantum Hilbert space (that is why those spaces are important in physics) show the link between the Shannon entropy to the Boltzmann, Gibbs and Von Neumann entropies (link to physics) Most of these ideas are from our paper: https://arxiv.org/abs/1912.02012 which is part of our bigger project Assumptions of Physics: https://assumptionsofphysics.org/